Equation Of Ellipse Having Foci On Y Axis
Y mx c.

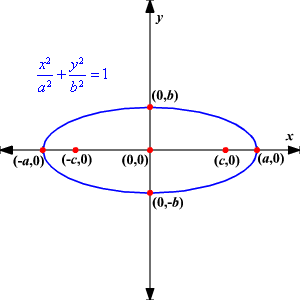
Equation of ellipse having foci on y axis. If cartesian coordinates are introduced such that the origin is the center of the ellipse and the x axis is the major axis and the foci are the points. The set of all points x y in a plane the sum of whose distances from two fixed points called foci is constant. Figure 1 shows a picture of an ellipse. An ellipse equation in conics form is always 1.
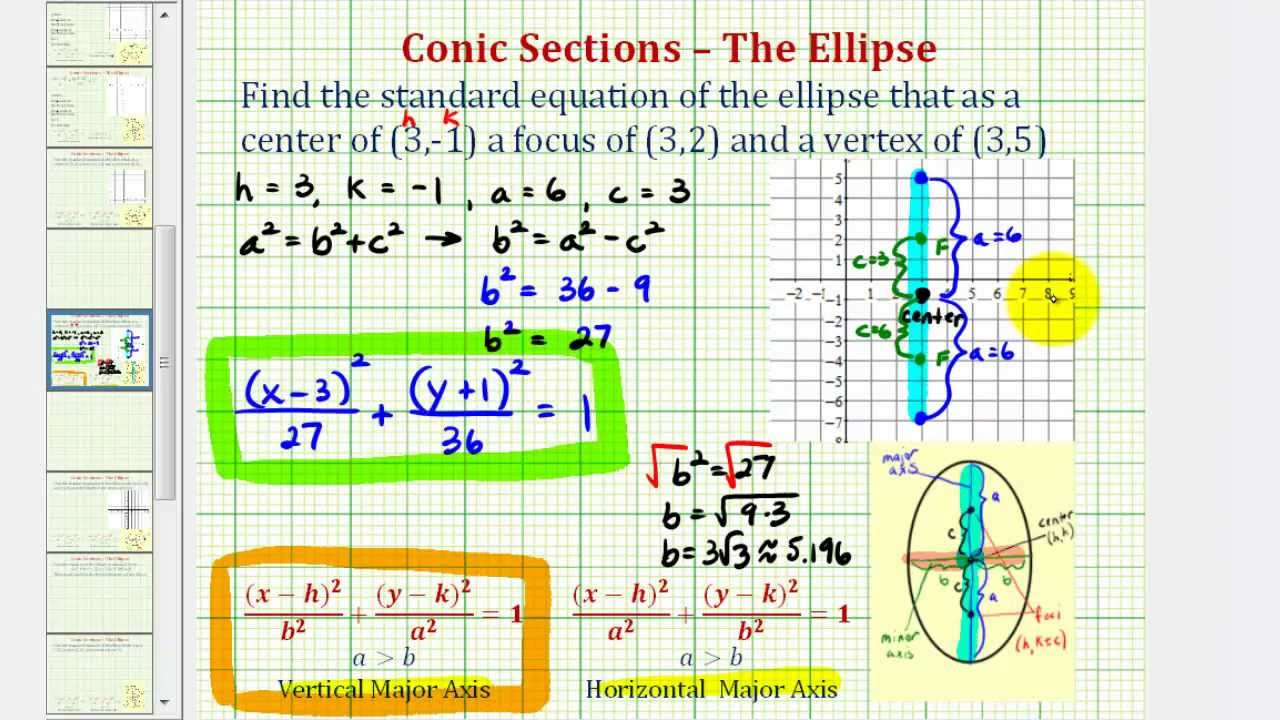
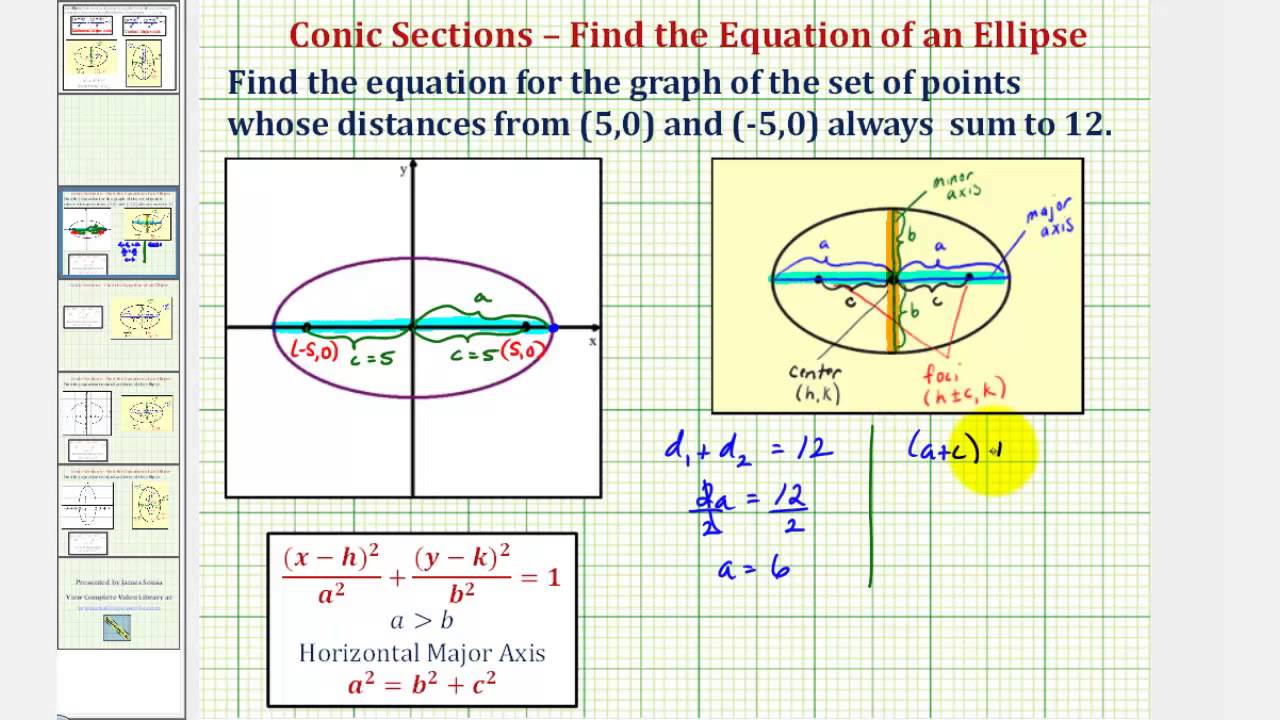
Note that in both equations above the h always stayed with the x and the k always stayed with. An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r2 from two fixed points f1 and f2 the foci separated by a. The word ellipse is derived from the greek word elleipsis defect. The same defect do we find in the linguistic ellipse.
Omitting a part of a sentence in situations. Solved examples of ellipse. Find the points on the ellipse x 2 3y 2 6 where the tangent are equally inclined to the axes. Prove also that the length of.
For parallel lines m 2 m 1 for perpendicular lines m 1 m 2 1 equation of straight line slope m i intercept c on real y axis.