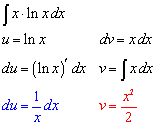Integration By Parts Formula
And from that were going to derive the formula for.
Integration by parts formula. In calculus and more generally in mathematical analysis integration by parts or partial integration is a process that finds the integral of a product of functions. In this section we will be looking at integration by parts. Of all the techniques well be looking at in this class this is the technique that students are most. Integration by parts is a special method of integration that is often useful when two functions are multiplied together but is also helpful in.
Integration by parts is a technique for performing indefinite integration intudv or definite integration intabudv by expanding the differential of a product of. Using the formula for integration by parts example find z x cosxdx. Solution here we are trying to integrate the product of the functions x and cosx. When using the method of integration by parts.
The formula for the method of integration by parts is given by. This formula follows easily from the ordinary. What were going to do in this video is review the product rule that you probably learned a while ago.